Model for Improvement and Hill Climbing

Improvement and hill-climbing really do go together.

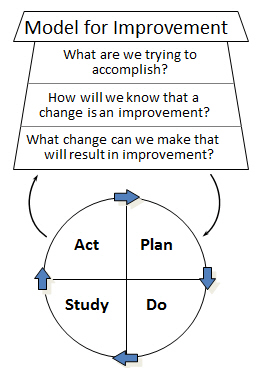
The Model for Improvement, codified by colleagues at API in the late 1980s as a general purpose guide to improvement, is actually an algorithm to reach a goal.   It combines three questions and a test cycle, as shown in the graphic from API.

One reason the Model for Improvement works as well as it does is that the Model tells you how to search for a goal. This claim is not just hand-waving, the Model for Improvement maps to a variety of learning or goal-seeking algorithms defined by computer scientists.

One of the simplest goal-seeking algorithms is the hill-climbing algorithm.

The hill-climbing search algorithm gives you a way to get to the top of a hill, starting from an arbitrary location.  You have an aim (reach the top of the hill), a way to measure progress (is a new location higher than the previous location?) and the ability to change--move from current location to new location.  So, you have the answers to the first three questions of the Model for Improvement:  aim, measurement, and change. 

There is a repeated cycle in the hill-climbing algorithm:  you evaluate options for a step up the hill, measure the height of each option relative to the current location, and take that option that is highest (and higher than the current location).   Repeat the cycle repeatedly until no further progress is detected.   This repeated cycle, along with the three answers essentially implements the Model for Improvement.

In the technical note at the end of this blog, I show how the Model for Improvement maps to another hill-climbing method, steepest ascent, which requires a few more assumptions than simple hill-climbing.

Sperm seeking an egg appear to deploy hill-climbing to reach the final destination, as described in this article in Science; goal-seeking behavior is fundamental to life.

Simple hill-climbing works if there is a single peak--no local peaks, no plateaus, no ridges that can get you stuck at a relatively low position relative to the absolute peak that is somewhere in the neighborhood.  Single peak system are common but not universal.

For example, a local peak means you've gotten system performance to a place where small changes only make things worse--but you're missing out on achieving substantially better performance with a different change that is not close by to where you're testing.  To get to the higher peak may require going downhill--accepting a short-term decline in performance-- to get in the neighborhood of the higher peak.

The way computer scientists modify simple hill-climbing is to restart the hill-climbing from different, random locations.   If a different starting position yields a better solution (higher on the hill), then the first hill top found is only a local maximum.   Starting from different locations corresponds to different initial conditions in a work system--so knowledge of starting conditions should inform our understanding of the impact of changes.  On the other hand, if different starting locations always yield the same ending point, your degree of belief that you have reached the highest point anywhere around should be strong.

Technical Note:  Model for Improvement and the Method of Steepest Ascent

Model for Improvement Item	Math version of a mountain climbing ("steepest ascent")	Notes
What is our aim?	Maximize a differentiable function F(x)	F(x) is the height of the function F at the point x
How do we know a change is an improvement?	Given a current position xi and a new position xi+1, we have an improvement if F(xi+1) > F(xi) and |F(xi+1) - F(xi)| > ε	We compare the height at the point xi+1 to the height at the point xi. So long as the heights differ by at least a little bit indicated by the value ε, then we are still increasing the height by moving from xi to xi+1.
What change can we make?	Choose xi+1 = xi + λi del(F)|i	del(F)|i is the multivariate “slope” of the function F, evaluated at the point xi. The equation says that we want to move to a new point xi+1 in the direction of increasing slope, by an amount given by the scale factor λ, when we start from point xi.
Cycle 1 Plan	Choose λ0 = 1 and some guess x0. Predict that if we set x1 = x0 + λ0 del(F)|0, then F(x1) will be greater than F(x0) and |F(x1) - F(x0)| > ε
Cycle 1 Do	Calculate F(x1), F(x0), del(F)|0 and |F(x1) - F(x0)|
Cycle 1 Study	Compare |F(x1) - F(x0)| to ε and compare F(x1) to F(x0). Do the predictions hold?—is F(x1) > F(x0) and |F(x1) - F(x0)| > ε?
Cycle 1 Act	If |F(x1) - F(x0)| ≤ ε, then stop. x1 is at least a local maximum. If F(x1) > F(x0), then let λ1= λ0 and x2 = x1 + λ1 del(F)|1. Go to Cycle 2 Plan. If F(x1) ≤ F(x0), then let λ1= λ0/2 and let x1 = x0 and x2 = x1 + λ1del(F)|1. Go to Cycle 2 Plan.	Properties of F (e.g. concavity) may indicate that the local maximum is a global maximum
Cycle 2 Plan	Same as Cycle 1 Plan but replace x0 with x1, x1 with x2 and del(F)|0 with del(F)|1
Cycle 2 Do	Same as Cycle 1 Do but replace x0 with x1 , x1 with x2 and del(F)|0 with del(F)|1
Cycle 2 Study	Same as Cycle 1 Study but replace x0 with x1 and x1 with x2.
Cycle 2 Act	Same as Cycle 1 Act but replace x0 with x1 and x1 with x2 and replace Cycle 2 Plan with Cycle 3 Plan, incrementing indices appropriately.
. . .

Keep going until the algorithm terminates--you will reach at least a local maximum.   As with the hill-climbing algorithm, you can start steepest ascent from various locations and see if the algorithm finds any other peak.